An Introduction to Artificial Neural Networks

James (and Jack) McKeown
mckeown@math.miami.edu
http://www.math.miami.edu/~mckeown
Machine Learning
  1. Supervised Learning
    • Learning from (input,output) pairs.
  2. Unsupervised Learning
    • Learning about data. (clustering)
    • No "right answer"
  3. Reinforcement Learning
    • Learning behavior from (possibly delayed) rewards and punishments.
What is an Artificial Neural Network (ANN)?
  • A directed acyclic graph of "neurons"
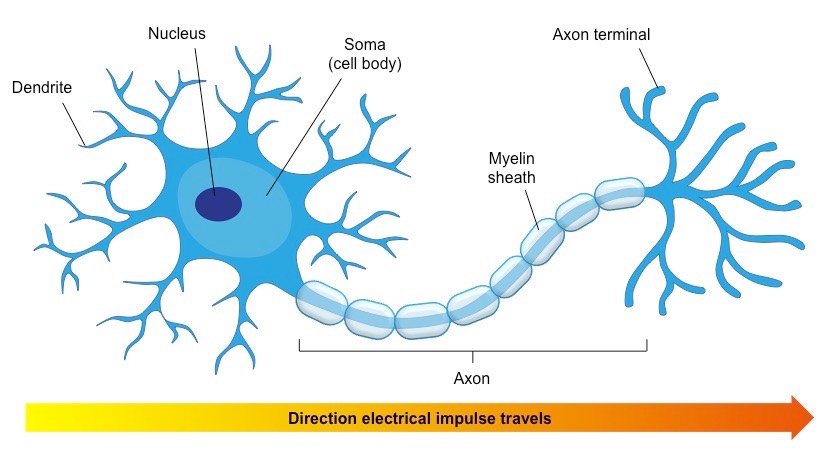
  • Inspired by biological neurons
  • A continuous and differentiable function
What is an artificial neuron?
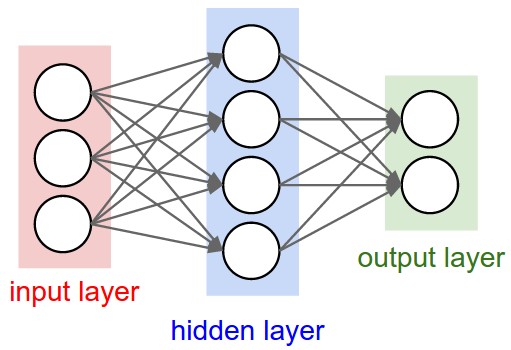
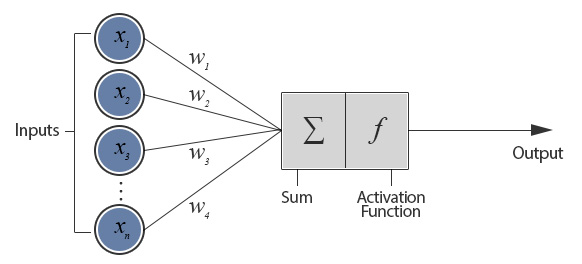
  • $f:\mathbb{R}^n\rightarrow\mathbb{R}$
  • $f(x) = \sigma(\displaystyle(\sum_{i=1}^n w_ix_i)+b) = \sigma(\vec{w}\cdot\vec{x}+b)$
What is $\sigma$?
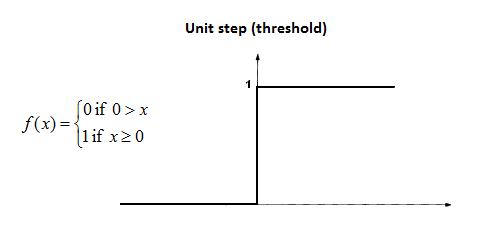
  • An "activation" function.
Boolean Operators with a Single Neuron
Training Neural Networks from Data!
Let's say we have a data set of $n$, $(\vec{x},\vec{y})$ pairs which are inputs and desired outputs, respectively.

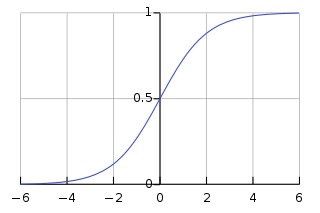
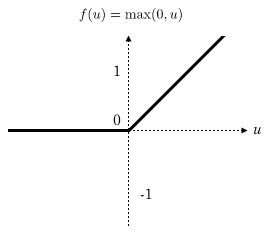
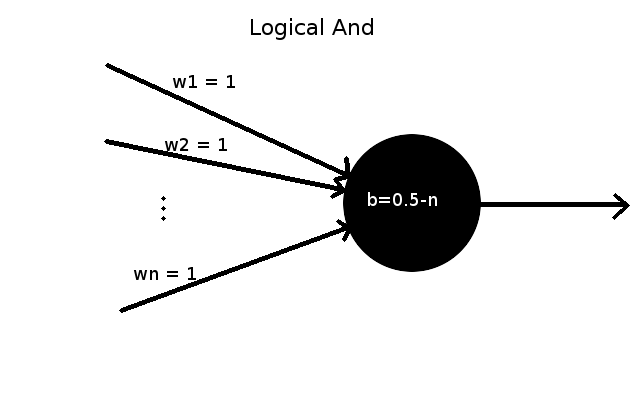
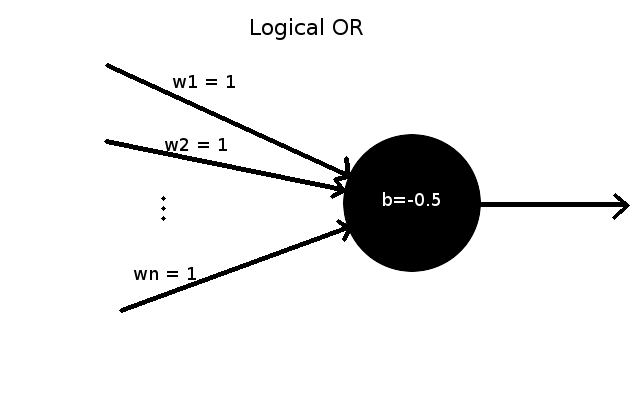
(Meaning we want $ f(\vec{x}) = \vec{y} $ for each $(\vec{x},\vec{y})$ pair after training)

Notation:
$ z^l = w^la^{l-1} + b^l $
$ a^l = \sigma(z^l) $
$ (a^0 = x, a^L \approx y)$
There are a few sensible ways to measure how bad our network is. We call this the cost,loss, or error.

For now we will use mean squared error: $ C = \displaystyle \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2 $

Idea: Let's start with a network of random weights and biases and then move them in the direction which reduces the error

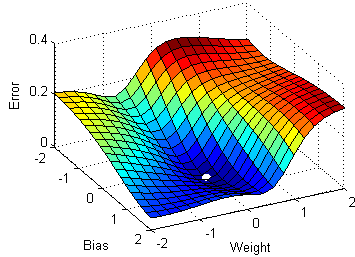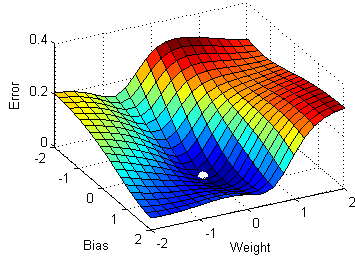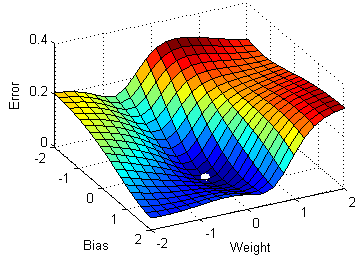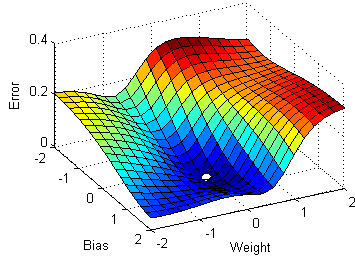
Gradient - direction of steepest ascent.
Want to find: $ \dfrac{\partial C}{\partial w^l_{jk}},\dfrac{\partial C}{\partial b^l_j} $

First let's find $\delta^l_j = \dfrac{\partial C}{\partial z^l_j}$ instead
Error in the Last Layer
$ \delta^L_j = \frac{\partial C}{\partial a^L_j}\frac{\partial a^L_j}{\partial z_j^L} = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) $

$ \delta^L = \nabla_{a^L} C \odot \sigma'(z^L)$

$ \delta^L = (a^L - y) \odot \sigma'(z^L)$

Error in the Last Layer
$ \delta^L = \underbrace{(a^L - y)}_{\nabla_{a^L}C} \odot \sigma'(z^L)$


Error in an Arbitrary Layer
$ \delta^l = \underbrace{((w^{l+1})^T \delta^{l+1})}_{\nabla_{a^l}C = \nabla_{z^{l+1}}C \odot \nabla_{a^l}z^{l+1}} \odot \sigma'(z^l)$
Error with respect to a Bias
$\frac{\partial C}{\partial b^l_j} = \delta^l_j$

$\frac{\partial C}{\partial b} = \delta$
Error with respect to a Weight
$\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j$
Code - Source
# numerical python library makes vector math efficient and easy
import numpy as np
s = lambda z: 1/(1+np.exp(-z)) #sigmoid activation function

X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T

# first weight matrix (3,4) means it's a 3x4 matrix
syn0 = 2*np.random.random((3,4)) - 1
# second weight matrix (4,1) means it's a 4x1 matrix
syn1 = 2*np.random.random((4,1)) - 1

for j in xrange(60000):
    l1 = s(np.dot(X,syn0))
    l2 = s(np.dot(l1,syn1))
    l2_delta = (y - l2)*(l2*(1-l2))
    l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))
    syn1 += l1.T.dot(l2_delta)
    syn0 += X.T.dot(l1_delta)
What next?

Teach computers to see!

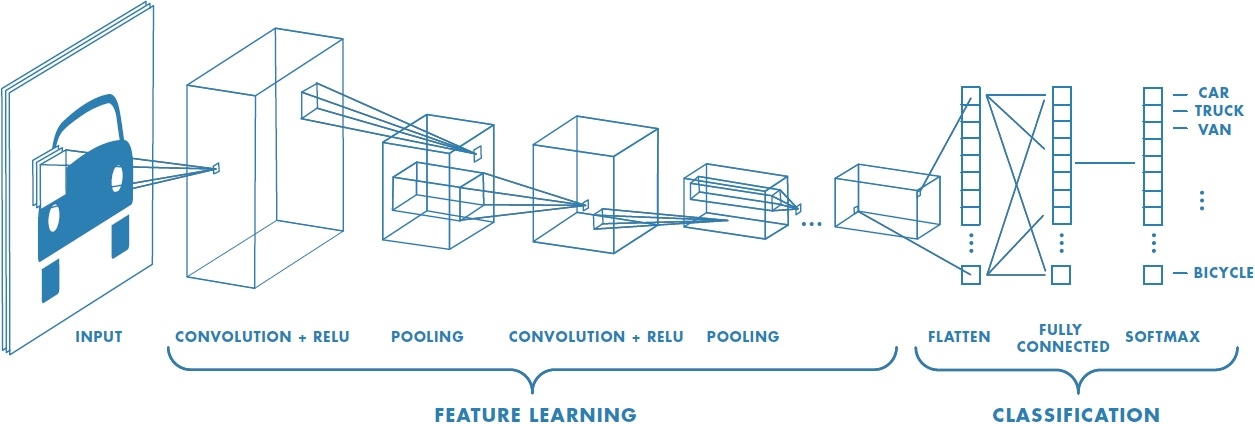Andrej Karpathy is the man...